Ejercicios sección 5.5

Utiliza la ley del seno o ley del coseno, para resolver los siguientes ejercicios.

  1. \hspace{0.1cm}Calcular la distancia que debe recorrer un obrero para subir y bajar una carretilla por una rampa. Si sabemos que la base mide 30 metros y tiene una inclinación de 30∘30^{\circ} en la subida y 45∘45^{\circ} en la bajada.
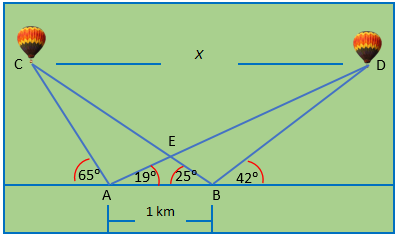
  2. \hspace{0.1cm}Dos observadores desde puntos distintos, ven dos globos, que están en el mismo plano vertical en el cual están ellos. La distancia entre los observadores es de 1 Km como lo muestra la figura. Hallar la distancia “xx” entre los dos globos.
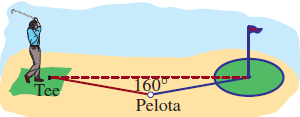
  3. \hspace{0.1cm}Ángulo de golpeo La distancia del tee al green de un determinado hoyo de golf es de 370 yardas. Un golfista realiza su primer golpe y coloca la pelota a 210 yardas del hoyo. Desde el punto donde se encuentra la pelota, el golfista mide un ángulo de 160∘160^{\circ} entre el tee y el green. Obtenga el ángulo de golpeo desde el tee medido desde la línea punteada que va del tee al green y que se muestra en la figura.
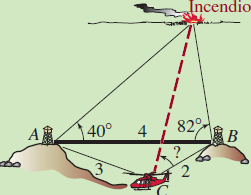
  4. \hspace{0.1cm}Dos torres vigía están situadas en las cumbres de las montañas A y B, a 4 millas de distancia. Un equipo de bomberos en helicóptero está en un valle en el punto C, a 3 millas de A y a 2 millas de B. Usando la línea entre A y B como referencia, un vigía ve un incendio en un ángulo de 40∘40^{\circ} de la torre A, y a 82∘82^{\circ} de la torre B, como se muestra en la figura. ¿A qué ángulo, medido a partir de CB, debe volar el helicóptero para dirigirse hacia el incendio?.
  5. \hspace{0.1cm}Ruta de un funicular. En la figura se ilustra un funicular que lleva pasajeros de un punto A, que está a 1.2 millas de un punto B en la base de una montaña, a un punto P en la cima de la montaña. Los ángulos de elevación de P de A y B son 21∘21^{\circ} y 65∘65^{\circ}, respectivamente.

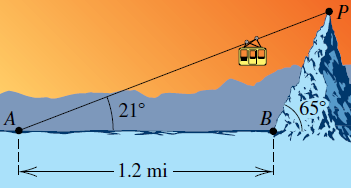
    6. a.\hspace{0.1cm}Calcule la distancia entre A y P.

    b.\hspace{0.1cm}Calcule la altura de la montaña.

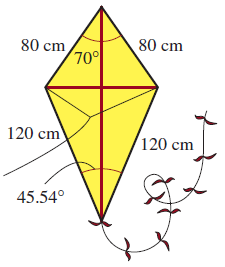
  6. \hspace{0.1cm}Cometa. Para el cometa que se muestra en la figura, determine las longitudes de las dos cañas que se requieren para los soportes diagonales.
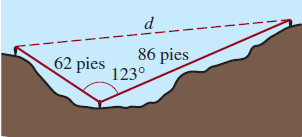
  1. \hspace{0.1cm}Anchura de un cañón Desde el suelo de un cañón se necesitan 62 pies de soga para alcanzar la cima de la pared del cañón y 86 pies para alcanzar la cima de la pared opuesta, como se muestra en la figura. Si las dos sogas forman un ángulo de 123∘123^{\circ} , ¿cuál es la distancia dd desde la cima de una pared del cañón a la otra?
  2. \hspace{0.1cm}Un bote pesquero mercante utiliza un equipo de sonar para detectar un banco de peces a 2 millas al este del bote y que se desplaza en la dirección N51∘51^{\circ}W a razón de 8mih8 \frac{mi}{h}, como se muestra en la figura.

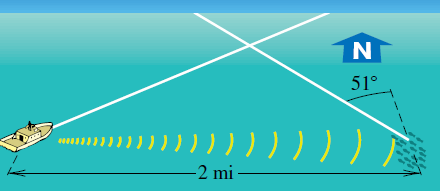
    3. a. \hspace{0.1cm}Si el bote navega a 20mih20\frac{mi}{h}, calcule, al 0.1∘0.1^{\circ} más cercano, la dirección a la que debe dirigirse para interceptar el banco de peces.

    b. \hspace{0.1cm}Encuentre, al minuto más cercano, el tiempo que tardará el bote en llegar a los peces.

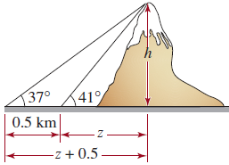
  3. \hspace{0.1cm}Un topógrafo usa un instrumento llamado teodolito para medir el ángulo de elevación entre el nivel del piso y la cumbre de una montaña. En un punto, se mide un ángulo de elevación de 41∘41^{\circ}. Medio kilómetro más lejos de la base de la montaña, el ángulo de elevación medido es de 37∘37^{\circ}, como se muestra en la figura. ¿Qué altura tiene la montaña?
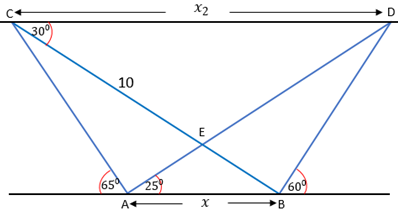
  4. \hspace{0.1cm}Con la información suministrada en la siguiente figura, encontrar el valor de x∧x2x\wedge x_2. Tener en cuenta que la distancia entre C y E es 10